Solução do 2º Teste, versão B, 2016/01/04
-
Calcule, se existirem em $\overline{\mathbb{R}}$, os seguintes limites:
- $\displaystyle \lim_{x\to 1}\frac{\log (1-x)}{\log (\sen (1-x))}$,
- $\displaystyle \lim_{x\to \pi/2}\,\left(\frac{2x}{\pi}\right)^{1/\cos x}$.
- Usando a regra de Cauchy \begin{align*} \lim_{x\to 1}\frac{\log (1-x)}{\log (\sen(1-x))} & =\lim_{x\to 1}\frac{-1/(1-x)}{\frac{-\cos(1- x)}{\sen(1-x)}} = \lim_{x\to 1} \frac{\sen(1-x)}{1-x} = 1. \end{align*}
- Temos uma indeterminação do tipo $1^\infty$; tem-se \[\left(\frac{2x}{\pi}\right)^{1/\cos x} = e^{\frac{\log(2x/\pi)}{\cos x}}.\] Consideramos então, usando regra de Cauchy, \[ \lim_{x\to \frac{\pi}{2}} \frac{\log(2x/\pi)}{\cos x} = \lim_{x\to \frac{\pi}{2}} \frac{\frac{1}{x}}{-\sen x}=-\frac{2}{\pi}\] pelo que graças à continuidade da função exponencial \[\lim_{x\to \pi/2}\,\left(\frac{2x}{\pi}\right)^{1/\cos x} = e^{-\frac{2}{\pi}}.\]
-
-
Determine uma primitiva de cada uma das seguintes funções:
- $\dfrac{\sen x}{2\cos x+5}$,
- $\dfrac{\arctg^3 x}{1+x^2}$.
- \[\int \frac{\sen x}{2\cos x+5}\, dx = -\frac{1}{2}\log|2\cos x+5|=-\frac{1}{2}\log(2\cos x+5)\]
- \[\int \frac{\arctg^3 x}{1+x^2} \, dx = \frac{1}{4}\arctg^4 x.\]
-
Calcule \[ \int^{1}_{0}\dfrac{e^{3x}}{1+e^{x}}\,dx. \]
Considerando a substituição $u=e^x$ obtém-se \begin{align*} \int^{1}_{0}\frac{e^{3x}}{1+e^x}\,dx & = \int_1^{e} \frac{u^3}{1+u} \frac{1}{u}\, du = \int_1^{e} \frac{u^2}{1+u} \, du \\ &= \int_1^{e} u-1 + \frac{1}{1+u} \, du = \left.\left[\frac{u^2}{2}-u+\log|1+u|\right]\right|^e_1 \\ &= \frac{e^2}{2}- e+ \log(1+e)-\frac{1}{2}+1-\log2 \\ &=\frac{e^2}{2}- e+\frac{1}{2}+\log\frac{1+e}{2}. \end{align*}
-
-
Calcule a área da região plana definida por \[ \left\{(x,y)\in\mathbb{R}^2: x\geq 0 \text{ e } \pi-2\arctg x \geq y\geq 2\arctg x\right\}. \]
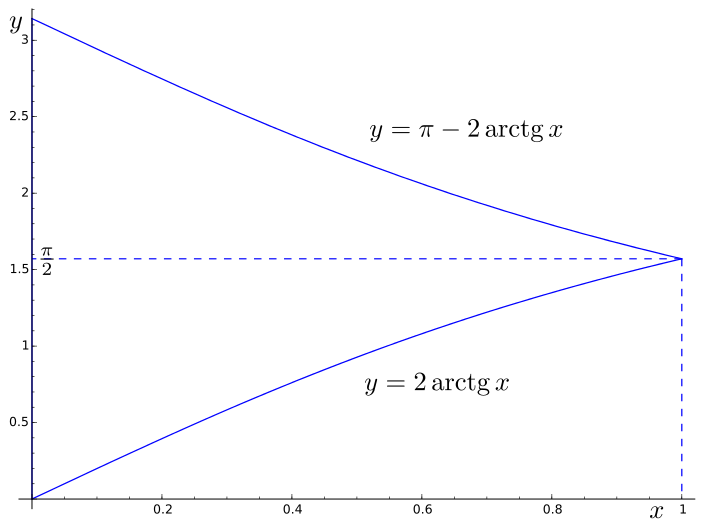
Temos $2\arctg x \leq \pi-2\arctg x \Leftrightarrow \arctg x \leq \frac{\pi}{4} \Leftrightarrow x\leq 1$. Daí que a região pretendida seja a esboçada na figura cuja área é \begin{align*} \int_0^1 (\pi-2\arctg x - 2\arctg x )\, dx & = \pi - 4 \int_0^1 \arctg x \, dx \\ & = \pi - 4\left.\left[x\arctg x \right]\right|_{x=0}^{x=1} + 4 \int_0^1 \frac{x}{x^2+1}\, dx \\ & = 2 \left.\left[ \log(x^2+1) \right]\right|_{x=0}^{x=1} = 2 \log 2 \end{align*} -
Seja $f:\mathbb{R} \to \mathbb{R}$ uma função contínua. Seja $g:\mathbb{R} \to \mathbb{R}$ a função definida por \[ g(x)=\int^{x}_{2} (2-x)\,f(t)\,dt. \]
- Supondo que $f$ é uma função positiva, mostre que $g(x)\leq 0$ para todo o $x\in \mathbb{R}$.
- Justifique que $g$ é diferenciável e calcule $g'$.
- Supondo que $f$ é uma função ímpar e $f(-2)=1$, calcule $g(-2)$ e $g'(-2)$.
- Se $x\geq 2$ temos $2-x\leq 0$ e $\int^{x}_{2} f(t)\,dt\geq 0$, donde $g(x)\leq 0$ se $x\geq 2$. Analogamente, se $x\leq 2$ temos $2-x\geq 0$ e $\int^{x}_{2} f(t)\,dt=-\int^{2}_{x} f(t)\,dt\leq 0$, donde $g(x)\leq 0$ se $x\leq 2$.
- Temos \[g(x)=\int^{x}_{2} (2-x) f(t)\,dt= (2-x) \int^{x}_{2} f(t)\,dt \] donde podemos derivar, usando o teorema fundamental do cálculo, \[ g'(x)=- \int^{x}_{2} f(t)\,dt + (2-x) f(x). \]
- Temos, usando ser $f$ uma função ímpar, \begin{align*} g(-2) & = \int^{-2}_{2} (2-(-2)) f(t)\,dt \\ & =4\left( \int^{0}_{2} f(t)\,dt + \int^{-2}_{0} f(t)\,dt\right)\\ & =4\left( \int^{0}_{2} f(t)\,dt + \int^{2}_{0} (-1)f(-t)\,dt\right)\\ &=4\left( \int^{0}_{2} f(t)\,dt + \int^{2}_{0} f(t)\,dt\right)=0, \\ g'(-2) & =- \int^{-2}_{2} f(t)\,dt + (2-(-2)) f(-2)= 4. \end{align*}
-
Estude quanto à natureza (convergência simples, absoluta e divergência) as séries seguintes:
- $\displaystyle\sum^{+\infty}_{n=1} \frac{n}{(n+5)\sqrt{n^2+1}}$,
- $\displaystyle\sum^{+\infty}_{n=2} \dfrac{1}{\sqrt {n^5}}\;\cos \left(\frac{\pi}{n}\right)$,
- $\displaystyle\sum^{+\infty}_{n=1} \dfrac{3n^4+1}{n!}$.
- Sabe-se que a série $\sum \frac{1}{n}$ é divergente. Como \[\lim \frac{\frac{1}{n}}{ \frac{n}{(n+5)\sqrt{n^2+1}}}= 1\] a série $\sum^{+\infty}_{n=1} \frac{n}{(n+5)\sqrt{n^2+1}}$ também é divergente.
- Como, para todo o $n\in\mathbb{N_2}$, $\left|\frac{1}{\sqrt {n^5}}\cos \left(\frac{\pi}{n}\right)\right|\leq \frac{1}{\sqrt {n^5}}$ e $\sum\frac{1}{n^{5/2}}$ é convergente, podemos concluir que a série $\sum^{+\infty}_{n=2} \dfrac{1}{\sqrt {n^5}}\;\cos \left(\frac{\pi}{n}\right)$ é absolutamente convergente.
- Como $\frac{1}{n!}\leq \frac{3n^4}{n!}$ basta provar que $\sum^{+\infty}_{n=1} \frac{n^4}{n!}$ é convergente. Tomando $a_n=\frac{n^4}{n!}$ temos \[\lim \frac{a_{n+1}}{a_n}= \lim \frac{1}{n+1} \frac{n^4}{(n+1)^4}=0<1\] donde se pode concluir que a série $\sum^{+\infty}_{n=1} \frac{3n^4+1}{n!}$ é (absolutamente) convergente.
Em alternativa:
Aplicar (directamente) o Critério de D'Alembert à série dada.
-
Seja $\phi \in C^2(\mathbb{R}^+)$ tal que $\phi'(1)=0, \phi''(1)=2$. Sendo $\varphi(x)=\phi(e^x)$, calcule \[
Temos \begin{align*} \varphi'(x) & =\phi'(e^x)e^x, \\ \varphi'(0) & =\phi'(1)=0, \\ \varphi''(x) & =\phi''(e^x)e^{2x}+\phi'(e^x)e^x, \\ \varphi''(0) & =\phi''(1)+\phi'(1)=2. \end{align*}Então, da Regra de Cauchy, \begin{align*} \lim_{x\to 0}\frac{\varphi(x)-\varphi(0)}{x^2}=\lim_{x\to 0}\frac{\varphi'(x)}{2x}& =\lim_{x\to 0}\frac{\varphi''(x)}{2}= 1.\end{align*}
\lim_{x\to 0}\frac{\varphi(x)-\varphi(0)}{x^2}.\]
Em alternativa:
Pelo teorema de Taylor, para $\varphi$ diferenciável numa vizinhança de $0$ e duas vezes diferenciável em $0$, temos \[ \lim_{x\to 0}\frac{\varphi(x)-\varphi(0)-\varphi'(0)x-\frac{1}{2}\varphi''(0)x^2 }{x^2}=0 \] o que implica \[ \lim_{x\to 0}\frac{\varphi(x)-\varphi(0)-x^2 }{x^2}=0 \] o que por sua vez garante \[ \lim_{x\to 0}\frac{\varphi(x)-\varphi(0)}{x^2}=1. \]
Última edição desta versão: João Palhoto Matos, 05/12/2017 14:38:13.
