Uma nota sobre integração

O que se segue é uma lista de tópicos relativos a integração que é imprescindível conhecer e uma lista de problemas seleccionados.

O significado da integração

É difí­cil descrever o significado de integração em linguagem leiga sem entrar em considerações de carácter técnico. E depois de entendermos o conceito de integração acabamos percebendo que tem um significado para além daquilo que inicialmente considerámos. A minha melhor tentativa talvez seja dizer que a diferenciação lida com a obtenção de uma função que descreve a variação de uma quantidade em função de outra e que a integração de alguma forma lida com o processo inverso. Claro que isto é demasiado vago e impreciso para ser efectivamente útil pelo que passemos para algo minimamente preciso.

Definição de integral

Lidamos com circunstâncias muito particulares do que acabaremos por chamar um integral. Consideramos funções limitadas definidas em intervalos limitados (e fechados mas o facto do intervalo ser fechado é essencialmente irrelevante) \(f:[a,b]\subset\mathbb{R}\to\mathbb{R}\), com \( a < b \). Chamamos partição de \([a,b]\) a um subconjunto finito de pontos de \([a,b]\) incluindo \(a\) e \(b\) que definem de forma natural uma famí­lia de subintervalos fechados de \([a,b]\) com interiores disjuntos dois a dois. Vai interessar-nos numerar os pontos da partição como segue \(a=x_0<x_1<x_2<\dots<x_k=b\) para uma partição de \(k+1\) pontos. Note-se que o número de pontos da partição é variável. Consideramos o conjunto de todas as possíveis partições de um intervalo \([a,b]\) designando-o por \(\mathcal{P}[a,b]\).

Fixada uma partição \(P\in\mathcal{P}[a,b]\) calculamos dois números:

\[S(f,P)=\sum_{i=0}^{k-1} (x_{i+1}- x_i) \sup_{[x_i,x_{i+1}]}f ,\] a soma superior de \(f\) relativa a \(P\),

\[s(f,P)=\sum_{i=0}^{k-1} (x_{i+1}- x_i) \inf_{[x_i,x_{i+1}]}f ,\] a soma inferior de \(f\) relativa a \(P\).

Deixando variar \(P\in\mathcal{P}[a,b]\) consideramos ainda

\[\overline{\int_a^b} f = \inf_{P\in\mathcal{P}[a,b]}S(f,P),\] o integral superior de \(f\) em \([a,b]\) e

\[\underline{\int_a^b}f = \sup_{P\in\mathcal{P}[a,b]}s(f,P),\] o integral inferior de \(f\) em \([a,b]\)

Dizemos que \(f\) é integrável em \([a,b]\) se o integral superior e o integral inferior coincidirem e nesse caso chama-se integral de \(f\) em \([a,b]\), denotado \(\int_a^b f\), ao valor comum. Caso contrário \(f\) diz-se não integrável em \([a,b]\).

De notar que esta descrição da definição de integral requer alguma verificação de coerência da definição. Por exemplo é preciso garantir que o integral a existir será um número real e não \(+\infty\) ou \(-\infty\).

A notação na definição de integral pode parecer pesada mas muito simplesmente envolve ideias muito antigas sobre o cálculo de áreas. Um esboço gráfico do significado da diferença entre soma superior e soma inferior será extremamente útil para perceber o que significa existir um integral.

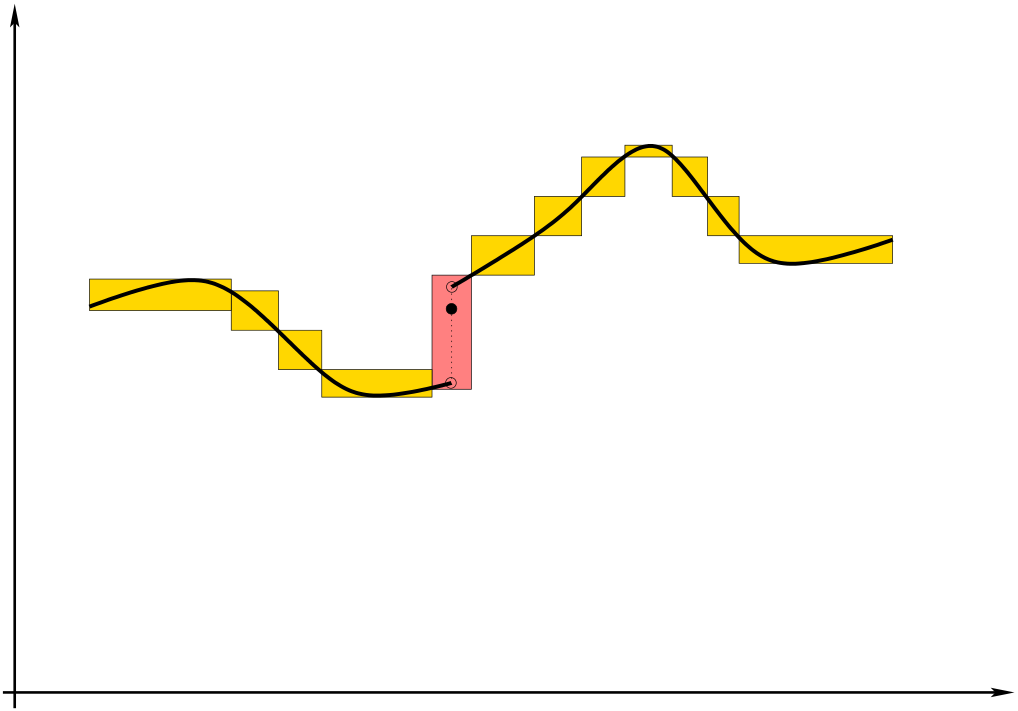
Deverá ficar relativamente claro que a integrabilidade de uma função, nas condições que estamos a considerar, corresponde a ter a possibilidade de cobrir o gráfico da função por uma família de rectângulos com soma de áreas arbitrariamente pequena. Se esboçar o gráfico de uma função e tentar fazê-lo suspeitará que a boa estratégia é cobrir porções do gráfico da função só com pontos de continuidade com rectângulos com "altura pequena" e tentar cobrir as porções do gráfico correspondentes com alguns pontos de descontinuidade com rectângulos cuja "soma de larguras" seja pequena. Também deve suspeitar que se de alguma forma houver "muitos" pontos de descontinuidade isto pode ser extremamente difí­cil ou até impossível. Que a discussão neste parágrafo se possa tornar precisa e ser usada para caracterizar as funções integráveis é um facto notável que de alguma forma tentaremos aclarar na secção seguinte.

As duas seguintes extensões do conceito de integral provarão ser computacionalmente úteis mais à frente: \[\int_a^a f=0, \qquad \int_b^a f= -\int_a^b f.\]

Que funções são integráveis?

Comecemos por um resultado positivo:

Teorema Seja \(f:[a,b]\to\mathbb{R}\) contí­nua. Então \(f\) é integrável em \([a,b]\).

Vaguíssima ideia da demonstração. Este resultado é dependente do teorema de Heine-Cantor e do conceito de continuidade uniforme. De uma forma altamente demagógica continuidade uniforme corresponde a poder controlar a oscilação de uma função num intervalo via o tamanho do intervalo e independentemente do centro desse intervalo. O teorema de Heine-Cantor simplesmente afirma que funções reais contínuas num intervalo limitado e fechado são uniformemente contí­nuas. Fim de vaguí­ssima ideia da demonstração.

Problema. Usando a ideia do resultado anterior e a definição de integral verifique que uma função limitada e descontí­nua num ponto, ou, mais geralmente, num número finito de pontos, é integrável.

De notar também que segue do mesmo raciocí­nio que o valor da função num número finito de pontos além de não afectar a integrabilidade também não afecta o valor do integral.

Uma função limitada descontí­nua num número infinito de pontos pode ser integrável.

Problema. Verifique que a função \(h:[0,1]\to\mathbb{R}\) definida por \[ h(x)=\begin{cases} 1, & \text{se } x=1/n, n\in\mathbb{N} \\ 0, & \text{se } x\neq 1/n, n\in\mathbb{N} \end{cases} \] é integrável. Determine o conjunto dos pontos de descontinuidade de \(h\).

Mas claro que há funções que não são integráveis.

Problema. Verifique que a função \(D:[0,1]\to\mathbb{R}\) definida por \[ D(x)=\begin{cases} 1, & \text{se } x\in\mathbb{Q}, \\ 0, & \text{se } x\not\in\mathbb{Q} \end{cases} \] não é integrável. Note que a função é descontí­nua em todo o intervalo \([0,1]\).

A existência de uma relação entre o conjunto dos pontos de descontinuidade de uma função e a sua integrabilidade é algo que não é objecto de estudo nesta disciplina. Posteriormente em CDI II voltaremos a este assunto. O resultado a que chegaremos será formulado em termos do conceito de medida nula.

Teorema. Uma função é integrável no sentido aqui apresentado se e só se o conjunto dos seus pontos de descontinuidade tiver medida nula.

Infelizmente para formularmos o conceito de medida nula precisávamos de já ter discutido a noção de série.

Combinando funções integráveis

São consequências fáceis da definição de integral:

Proposição (aditividade relativamente ao intervalo de integração) Sejam \(a< b< c \) números reais e \(f:[a,c]\to\mathbb{R}\) uma função limitada. Se as restrições de \(f\) a \([a,b]\) e a \([b,c]\) forem funções integráveis então \(f\) é integrável em \([a,c]\) e \[\int_a^c f= \int_a^b f + \int_b^c f.\] Reciprocamente se \(f\) for integrável em \([a,c]\) então é integrável em \([a,b]\) e \([b,c]\) valendo a igualdade anterior.

Proposição (o integral como funcional linear) O conjunto das funções reais de variável real integráveis num intervalo limitado e fechado \([a,b]\) forma um subespaço vectorial do espaço vectorial real das funções reais de variável real limitadas definidas nesse intervalo sendo o integral um funcional linear naquele subespaço.

Comentário. Em particular estamos dizendo que o produto de um real por uma função integrável é uma função integrável, a soma de funções integráveis é uma função integrável e dados \(\alpha, \beta \in\mathbb{R}\), \(f\) e \(g\) integráveis em \([a,b]\) então \(\alpha f + \beta g\) é integrável em \([a,b]\) e \[\int_a^b (\alpha f + \beta g)= \alpha \int_a^b f + \beta \int_a^b g\]

Ordem e desigualdades

ɉ uma consequência trivial da definição de integral:

Proposição Sejam \(a < b\) e \(f:[a,b]\to\mathbb{R}\) uma função integrável e tal que \(f\geq 0\). Então \[\int_a^b f \geq 0.\]

Usando a linearidade do integral é fácil concluir daqui que:

Corolário Sejam \(a < b\) e \(f,g:[a,b]\to\mathbb{R}\) funções integráveis e tais que \(f\geq g\). Então \[\int_a^b f \geq \int_a^b g.\]

Dada uma função real \(u\) definem-se a sua parte positiva \(u^+\) e a sua parte negativa \(u^-\) via \[u^+(x)=\begin{cases}u(x), & \text{ se } u(x)>0, \\ 0, & \text{ se } u(x)\leq 0, \end{cases}\] e \[u^-(x)=(-u)^+(x) =\begin{cases}-u(x), & \text{ se } u(x)<0, \\ 0, & \text{ se } u(x)\geq 0. \end{cases}\]

Note-se que \(u=u^+ - u^-\) e  \(|u|=u^+ + u^-\). Se \(u:[a,b]\to\mathbb{R}\) com \(a<b\) for integrável então pode tirar-se partido da desigualdade \[ 0\leq S(u^+,P)-s(u^+,P) \leq S(u,P)-s(u,P)\] válida para todo o \(P\in\mathcal{P}([a,b])\) para estabelecer que \(u^+\) é integrável e depois, por linearidade, que \(u^-\) e \(|u|\) são integráveis em \([a,b]\). Temos assim:

Proposição Seja \(a < b\) e \(f:[a,b]\to\mathbb{R}\) uma função integrável em \([a,b]\). Então \(|f|\) é integrável em \([a,b]\) com \[\left|\int_a^b f\right| \leq \int_a^b |f|.\]

 

Integral indefinido e teorema fundamental

Dada \(f:[a,b]\to\mathbb{R}\) integrável e \(c\in[a,b]\), definimos um integral indefinido de \(f\) em \([a,b]\) como sendo uma qualquer função da forma \[ [a,b]\ni x \mapsto \int_c^x f.\]

Problema. Verifique que um integral indefinido é uma função contí­nua.

Sugestão. Isto essencialmente segue da estimativa \( \left|\int_c^x f - \int_c^{x+h} f  \right|= \left|\int_x^{x+h}f\right|\leq |h| \sup |f| \). Fim de sugestão.

No caso de \(f\) ser contínua, uma pequena melhoria da estimativa anterior (notar que o \(\sup\) basta ser considerado no intervalo de extremos \(x\) e \(x+h\)) permite obter o resultado que de alguma forma esclarece aquilo que tínhamos afirmado no iní­cio desta nota.

Teorema (fundamental do cálculo) Dada \(f:[a,b]\to\mathbb{R}\) contínua e \(c\in[a,b]\), o integral indefinido \[ [a,b]\ni x \mapsto \int_c^x f\] é uma função diferenciável com derivada \(f\).

Relembrando que duas primitivas num intervalo diferem de uma constante e usando o resultado anterior obtemos uma regra de integração:

Teorema (regra de Barrow) Seja \(f:[a,b]\to\mathbb{R}\) contínua e \(F\) uma sua primitiva em \([a,b]\). Então \[F(b)-F(a)=\int_a^b f.\]

A regra de Barrow juntamente com as fórmulas de primitivação por partes e por substituição permite obter as chamadas fórmulas de integração por partes e por substituição. Voltaremos a elas nalguns dos exercícios que consideramos a seguir.

Problemas

Consideraremos os problemas seguintes se não houver sugestões, dúvidas,... Não há qualquer garantia implícita nesta lista de que sejam suficientes para testar os seus conhecimentos de cálculo integral.

Semana de 19/12/2011

Semana de 2/1/2012