Convexidade para funções reais de variável real
Este artigo pretende dar ênfase a uma definição geométrica de convexidade para funções reais de variável real e daí derivar as habituais propriedades de funções convexas duas vezes diferenciáveis.
Definição. Seja \(I\subset\mathbb{R}\) um intervalo e considere-se uma função com valores reais definida em \(I\), \(f:I\to \mathbb{R}\). Diz-se que \(f\) é convexa em \(I\) se para quaisquer \(a,b\in I\) e \(\theta\in [0,1]\) tivermos \[f(\theta a+(1-\theta)b)\leq \theta f(a)+(1-\theta)f(b).\] Diremos que \(f\) é côncava em \(I\) se \(-f\) for convexa.
O significado da definição corresponde, usando linguagem sugestiva mas imprecisa, a dizer que a interpolação linear entre dois pontos do gráfico da função está sempre acima do ponto do gráfico com a mesma abcissa.
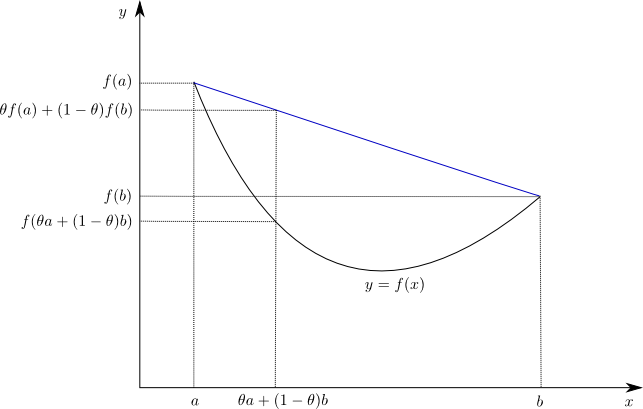
Exemplo. Qualquer função afim, isto é da forma \(x\mapsto ax+b\) com \(a, b\in\mathbb{R}\) números reais fixos é uma função simultaneamente convexa e côncava.
Exemplo. A função \(h:{[0,+\infty[}\to\mathbb{R}\) definida por \[\begin{cases}1, & \text{se } x=0,\\ 0, & \text{se } x>0, \end{cases}\] é uma função convexa.
Note-se que este exemplo anterior mostra que uma função convexa não é necessariamente contínua. No entanto
Proposição. Seja \(I\subset\mathbb{R}\) um intervalo aberto e considere-se uma função convexa com valores reais definida em \(I\), \(f:I\to \mathbb{R}\). Então \(f\) é contínua em \(I\).
Ideia da demonstração. Considere-se um ponto \(x_0\in I\) em que pretendemos mostrar que \(f\) é contínua e dois outros pontos do intervalo \(I\), \(a\lt x_0\lt b\).

De facto estabelecemos a partir da definição de convexidade que, se \(C=\max\left(\frac{\left|f(b)-f(x_0)\right|}{b-x_0},\frac{\left|f(a)-f(x_0)\right|}{x_0-a}\right)\), então para todo o \(x\in \left]a,b\right[\), temos \[\left|f(x)-f(x_0)\right|\leq C |x-x_0|.\] A partir desta condição é fácil provar que \(f\) é contínua em \(x_0\). Fim da ideia de demonstração.
Note-se que as funções convexas num intervalo aberto não são necessariamente diferenciáveis nos pontos desse intervalo. Com efeito
Exemplo. A função \(x\mapsto |x|\) é convexa em \(\mathbb{R}\) mas não é diferenciável em \(0\).
No entanto as derivadas direitas e esquerdas de uma função convexa num intervalo estão sempre definidas e, com a possível excepção dos extremos do intervalo, são finitas. Mais precisamente
Proposição (crescimento da razão incremental). Seja \(I\subset\mathbb{R}\) um intervalo e considere-se uma função convexa com valores reais definida em \(I\). Então, para qualquer ponto \(x_o\in I\), a função \(I\ni x\mapsto \frac{f(x)-f(x_0)}{x-x_0}\) é crescente em \(I\).
Demonstração: Exercício.
Corolário. Seja \(I\subset\mathbb{R}\) um intervalo aberto e considere-se uma função convexa \(f\) com valores reais definida em \(I\). Então, para todos os pontos \(x_0\in I\) existem e são finitas a derivada esquerda e a derivada direita de \(f\) em \(x_0\) com \[f'_e(x_0)\leq f'_d(x_0).\]
Ideia da demonstração do corolário: Da propriedade de crescimento estabelecida na proposição segue que \[f'_e(x_0) = \sup_{x\lt x_0}\frac{f(x)-f(x_0)}{x-x_0}\leq \inf_{x\gt x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'_d(x_0) .\] Fim da ideia de demonstração do corolário.
A propriedade de crescimento da razão incremental também implica
Corolário. Seja \(I\subset\mathbb{R}\) um intervalo aberto e considere-se uma função convexa \(f\) com valores reais definida em \(I\). Então a derivada esquerda e a derivada direita de \(f\) em \(I\) são funções crescentes.
No caso particular da função ser duas vezes diferenciável
Corolário. Seja \(I\subset\mathbb{R}\) um intervalo aberto e considere-se uma função convexa e duas vezes diferenciável \(f\) com valores reais definida em \(I\). Então \(f''\geq 0\) em \(I\).
Reciprocamente
Proposição. Seja \(I\subset\mathbb{R}\) um intervalo aberto e considere-se uma função duas vezes diferenciável \(f\) com valores reais definida em \(I\) verificando \(f''\geq 0\). Então \(f\) é convexa em \(I\).
Demonstração. De \(f''\geq 0\) decorre que \(f'\) é crescente em \(I\). Se \(f\) não fosse convexa em \(I\) existiriam \(a,b,c\in I\) com \(a\lt c\lt b\) tais que \(\frac{c-a}{b-a}f(b)+\frac{b-c}{b-a}f(a)\gt f(c)\). Do teorema de Lagrange aplicado a \(f\) em \([a,c]\) e em \([c,b]\) decorre que existem \(\alpha \in {]a,c[}, \beta \in {]c,b[}\) tais que \[\begin{align*}f'(\alpha) & =\frac{f(c)-f(a)}{c-a}, \\ f'(\beta) & =\frac{f(b)-f(c)}{b-c}.\end{align*}\] Mas tal implicaria que \(f'(\alpha)>f'(\beta)\) devido a \((*)\), contradizendo o crescimento de \(f'\). Fim de demonstração.
Podemos assim, à custa da análise do sinal da segunda derivada de uma função obter informação adicional pertinente para esboçar o respectivo gráfico.
Exemplo. Seja \(g:\mathbb{R}\to\mathbb{R}\) definida por \[g(x)=\frac{x}{1+x^2}.\] Pretende-se esboçar o gráfico de \(g\).
Começamos por notar que \(g\) é ímpar, isto é satisfaz \(g(-x)=-g(x)\) para todo o \(x\in\mathbb{R}\), pelo que o seu gráfico será simétrico relativamente a \((0,0)\) bastando-nos, se necessário, fazer cálculos para \(x\geq 0\).
Sendo uma função racional \(g\) é indefinidamente diferenciável e temos \[\begin{align*}g'(x) &=\frac{1+x^2-2x^2}{(1+x^2)^2} = \frac{1-x^2}{(1+x^2)^2} \\ g''(x) & = \frac{-2x(1+x^2)^2 - (1-x^2)2(1+x^2) 2 x}{(1+x^2)^4}=\frac{-2x(1+x^2) - (1-x^2)4 x}{(1+x^2)^3}= \frac{-6x + 2 x^3}{(1+x^2)^3}\end{align*}\]
Analisando o sinal de \(g'\) verificamos que \(g\) é crescente para \(x\in [0,1]\) e decrescente em \([1,+\infty[\). Analisando o sinal de \(g''\) verificamos que \(g\) é convexa em \([\sqrt{3},+\infty[\) e côncava em \([0,\sqrt{3}]\). Observe-se que a informação de crescimento e convexidade para \(x<0\) decorre de \(g'\) ser par e \(g''\) ser ímpar (prove que tal é sempre verdade para a primeira e segunda derivada de uma função ímpar duas vezes diferenciável).
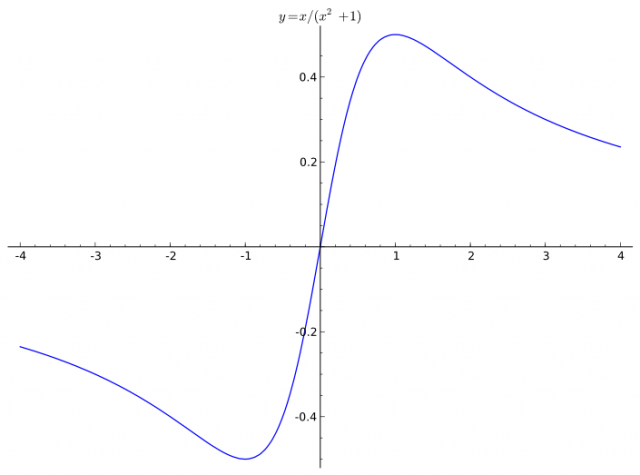
Note também que \(g\) satisfaz \[\lim_{x\to+\infty}g(x)= \lim_{x\to-\infty}g(x)=0\] algo que com a escala usada na figura gerada numericamente dificilmente se intui.
Última edição desta versão: João Palhoto Matos, 08/09/2021 17:59:00.
